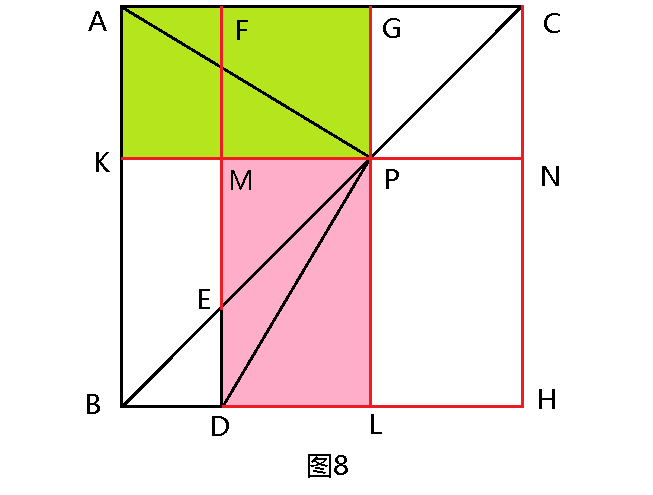
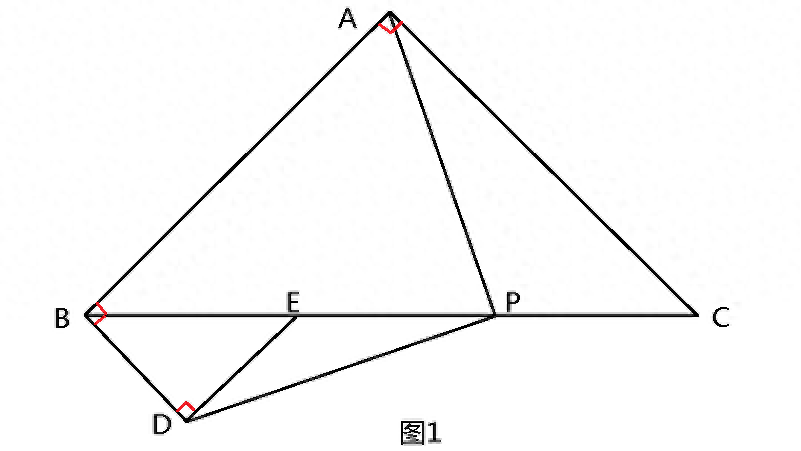
题目:如图1,在等腰Rt△ABC中,AB=AC,等腰Rt△BDE中,BD=DE,E在BC上,D在BC下方,P为EC的中点。证明:PA⊥PD。
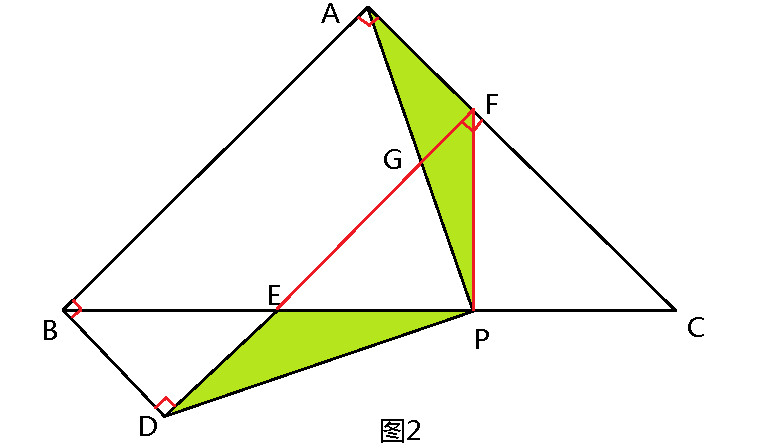
解题思路(1):延长DE交AC于F,交AP于G(图2)。
易证四边形ABDF为矩形,AF=BD=DE;Rt△EFC为等腰Rt△,PE=PF=PC。
易证△EDP≌△FAP,则∠EDP=∠FAP,DP=AP。
在Rt△AFG和△DPG中,∠EDP=∠FAP,∠DGP=∠AGF,
故∠DPG=∠AFG=90°,即PA⊥PD且PA=PD。
解题思路(2):延长DP至点F,使DP=PF(类似于倍长中线),连接FC、AD、AF(图3)。
易证△DEP≌△FCP,则CF=DE=DB,∠DEP=∠FCP=135°,∠ACF=90°。
易证Rt△ABD≌Rt△AFC,则AD=AF,
故△APD≌△APF,∠APD=∠APF=90°,PA⊥PD得证。
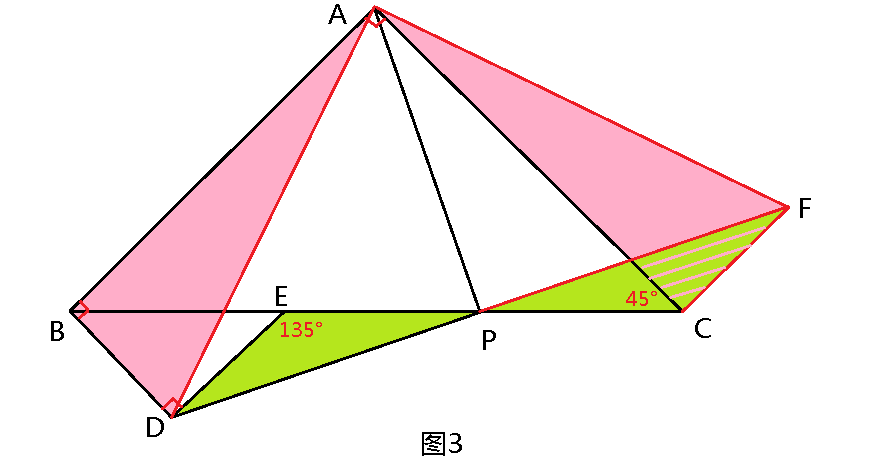
解题思路(3):连接AD,将△ABD绕点A逆时针旋转90°得到Rt△ACF,连接PF(图3)。具体证明类似解题思路(2)。
解题思路(4):欲证PA⊥PD,证明A、B、D、P四点共圆即可。
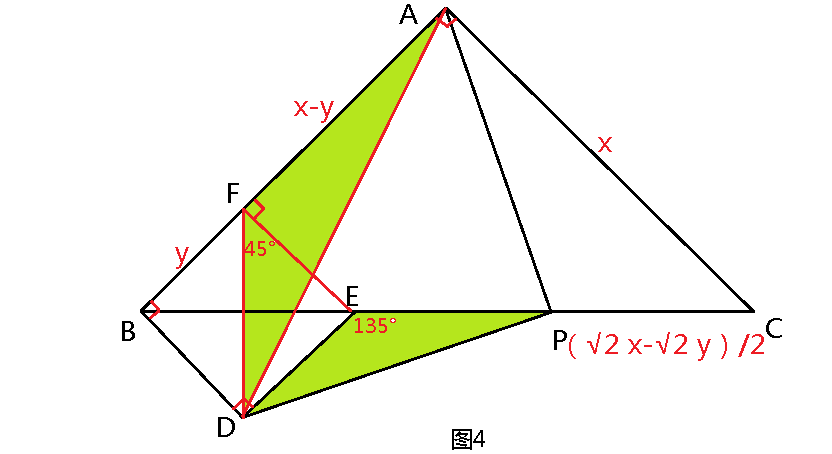
过点E作EF⊥AB,垂足为F(图4),则四边形EFBD为正方形;连接FD、AD,∠AFD=∠PED=135°。
设AB=AC=x,BC=√2x;
BF=DE=y,FD=BE=√2y,EP=(√2x-√2y)/2;
FA=x-y。
在△AFD和△PED中,FD/AF=(√2y)/(x-y);
DE/EP=y/{(√2x-√2y)/2}=(√2y)/(x-y),
结合∠AFD=∠PED,故△AFD∽△PED,
则∠FAD=∠EPD,故A、B、D、P四点共圆,
∠APD=180°-∠ABD=180°-90°=90°,
PA⊥PD成立。另外,∠DAP=∠DBP=45°,故Rt△APD亦为等腰Rt△,PA=PD。
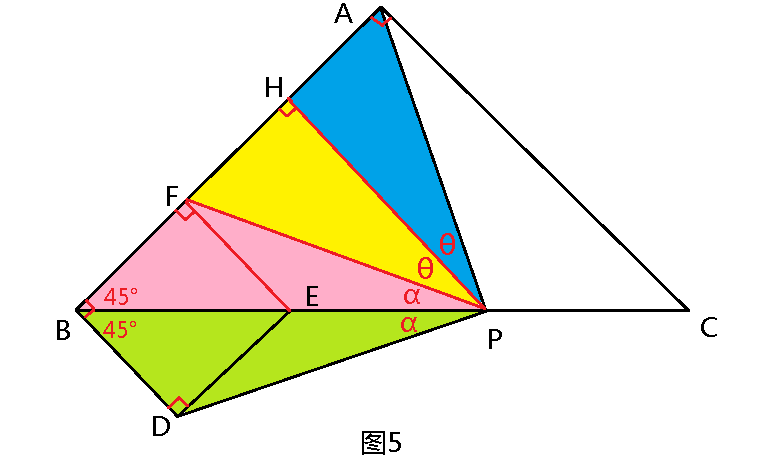
解题思路(5):过点E作EF⊥AB,垂足为F(图5),则四边形EFBD为正方形。
连接FP,易证△PFB≌△PDB,则PF=PD,∠DPB=∠FPB=α。
过点P作PH⊥AB,垂足为H。
在梯形AFEC中,PH∥EF∥CA,因P为EC的中点,根据“经过梯形一腰的中点与底平行的直线必平分另一腰”,则H为FA的中点,故PH为FA的垂直平分线,
PA=PF=PD,∠APH=∠FPH=θ。
因∠HPB=α+θ=45°,故∠APD=2(α+θ)=90°。
解题思路(6):作AH⊥BC,DG⊥BE,垂足分别为H、G(图6)。
设GB=GE=GD=m,PE=PC=n,BC=2(m+n),
则HB=HC=HA=1/2BC=m+n,
HC=HP+PC=HP+n=m+n,即HP=m。
在Rt△DGP和Rt△PHA中,HP=GD=m,AH=PG=m+n,
则Rt△DGP≌Rt△PHA,∠GPD=∠HAP,∠GDP=∠HPA,
故∠APD=∠HPA+∠GPD=∠HPA+∠HAP=90°,PA⊥PD成立。
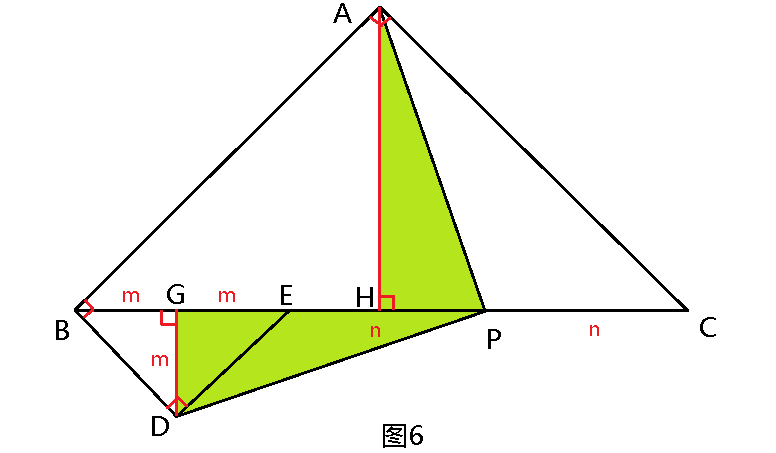
解题思路(7):如图6所示,AB=BC/√2=2(m+n)/√2=√2(m+n),BD=√2m。
易证AB²+BD²=AP²+PD²,根据勾股定理的逆定理,则∠APD=90°得证。
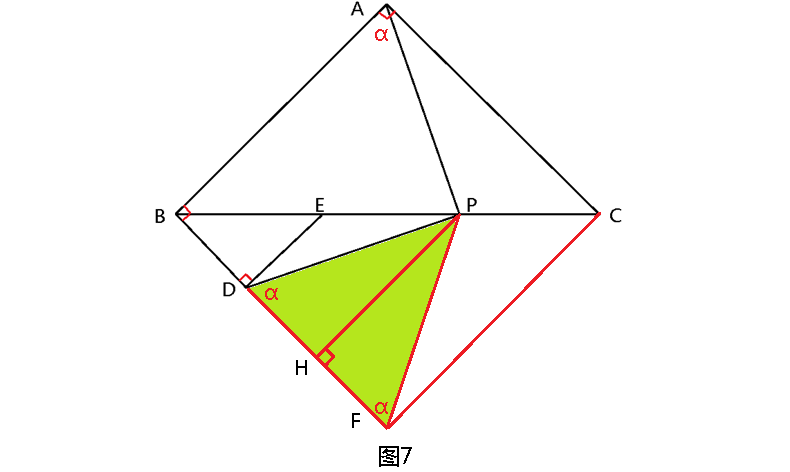
解题思路(8):补全等腰Rt△ABC、等腰Rt△BDE得到正方形ABFC,连接PF,作PH⊥BF(图7)。
易证△BAP≌△BFP,则PA=PF,∠BAP=∠BFP=α。
易证四边形EDFC为等腰梯形,PH为梯形的中位线,
故H为DF的中点,即PH为DF的垂直平分线,故
PD=PF=PA,∠PDF=∠PFD=∠BAP=α。
在四边形ABDP中,∠BDP+∠BAP=∠BDP+∠PDF=180°,则∠APD=360°-∠ABD-∠BDP-∠BAP
=360°-90°-180°=90°。
解题思路(9):补全等腰Rt△ABC、等腰Rt△BDE得到正方形ABHC(图8),过点P作平行于AB、AC的直线分别交正方形边长于G、L、K、N;过点E作EF⊥AC交KN于M。
在等腰Rt△EFC中,MP、PG均为中位线,易证矩形AKPG和矩形MDLP的两边长分别相等,其对角线AP、PD相等且垂直。